La façon dont un modèle d’apprentissage automatique s’adapte aux données est régie par un ensemble de conditions initiales appelées hyperparamètres. Les hyperparamètres aident à restreindre le comportement d’apprentissage d’un modèle afin qu’il puisse (espérons-le) bien s’adapter aux données et dans un délai raisonnable. Trouver le meilleur ensemble d’hyperparamètres (souvent appelé « réglage ») est l’une des parties les plus importantes et les plus chronophages de la tâche de modélisation. Les approches historiques du réglage des hyperparamètres impliquent soit une force brute, soit une recherche aléatoire sur une grille de combinaisons d’hyperparamètres appelées Grid Search et Random Search, respectivement. Bien que populaires, les méthodes de recherche par grille et aléatoire n’ont aucun moyen de converger vers un ensemble décent d’hyperparamètres – c’est-à-dire qu’elles ne sont que des essais et des erreurs.

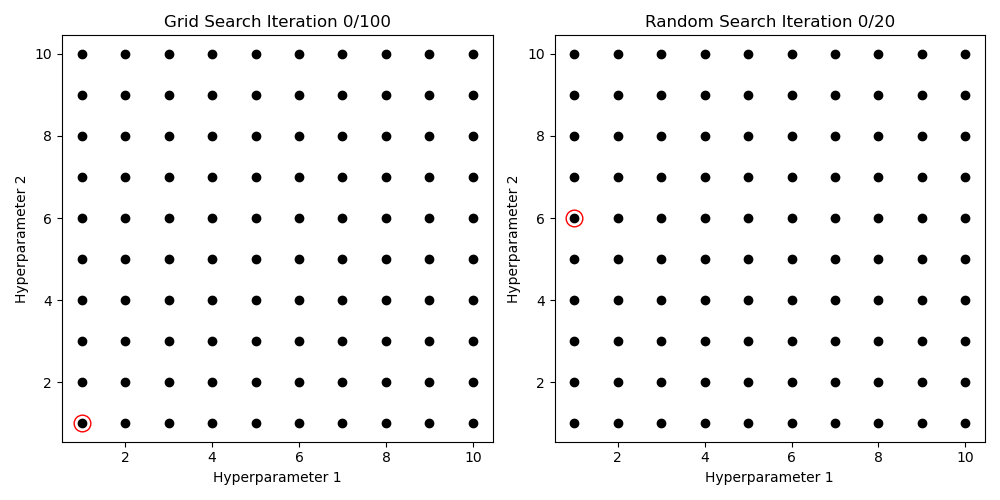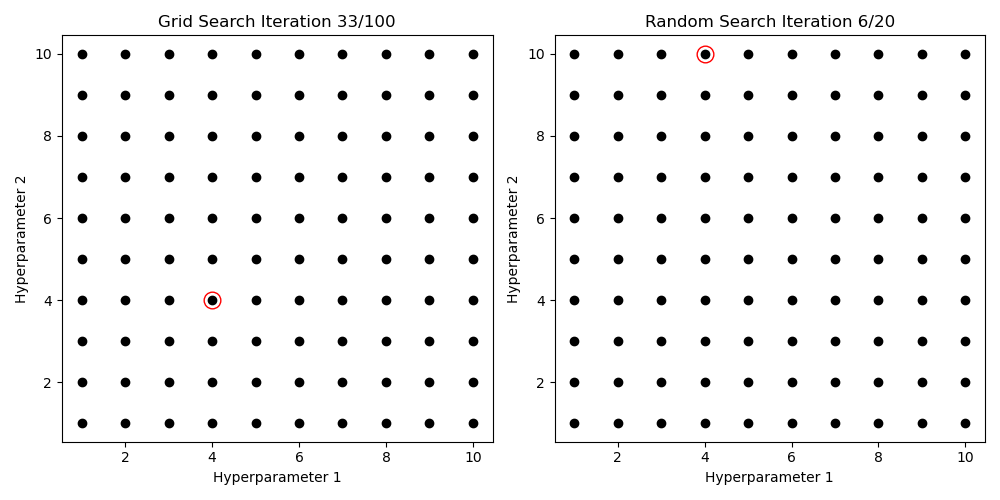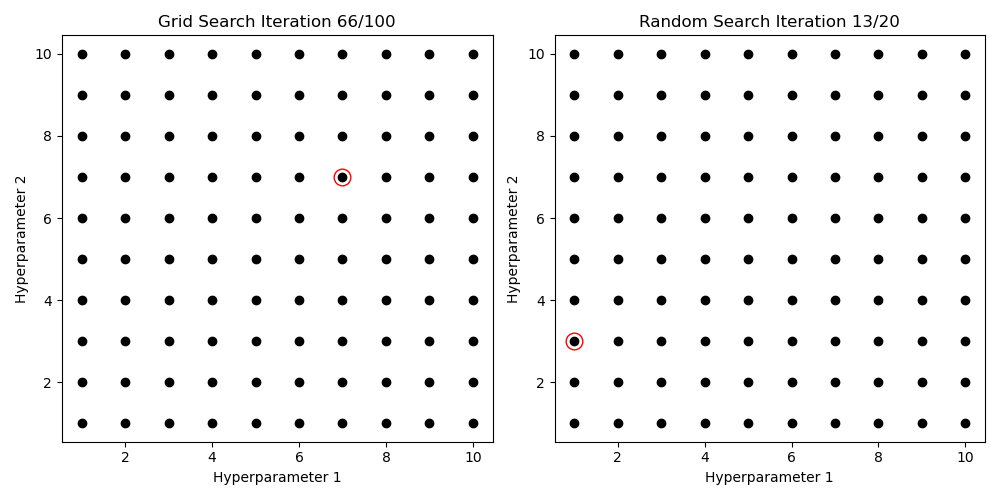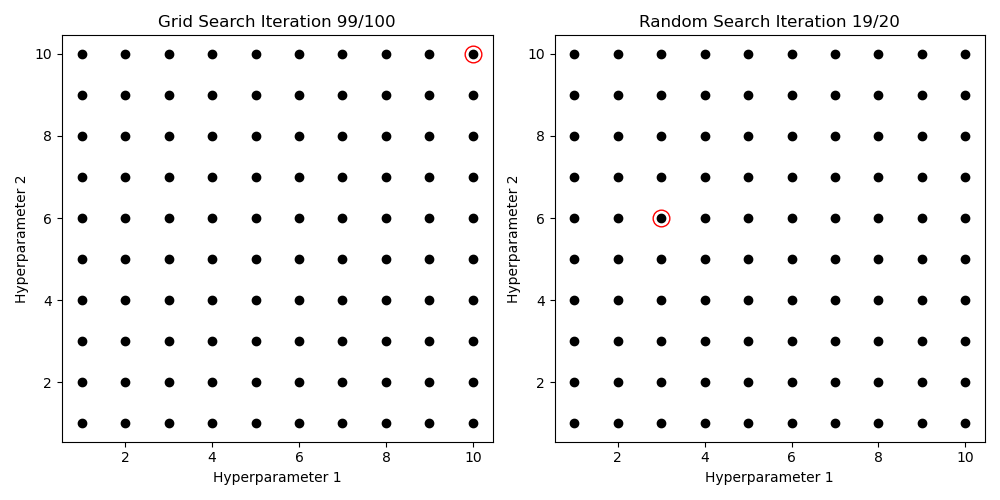
TPE est un algorithme d’optimisation bayésien. Cela signifie que cela nous permet de commencer par quelques croyances initiales sur ce que sont nos meilleurs hyperparamètres de modèle, et de mettre à jour ces croyances de manière fondée sur des principes au fur et à mesure que nous apprenons comment différents hyperparamètres ont un impact sur les performances du modèle. C’est déjà une amélioration significative par rapport à la recherche par grille et à la recherche aléatoire ! Au lieu de déterminer le meilleur ensemble d’hyperparamètres par essais et erreurs, au fil du temps, nous pouvons essayer plus de combinaisons d’hyperparamètres qui conduisent à de bons modèles et moins qui ne le font pas.

TPE tire son nom de deux idées principales : 1. utiliser l’estimation de Parzen pour modéliser nos croyances sur les meilleurs hyperparamètres (plus à ce sujet plus tard) et 2. utiliser une structure de données arborescente appelée graphe d’inférence postérieure pour optimiser le temps d’exécution de l’algorithme. Dans cet exemple, nous ignorerons la partie “arborescente” car elle n’a rien à voir avec le réglage des hyperparamètres en soi. De plus, nous n’entrerons pas dans le détail des statistiques bayésiennes, des améliorations attendues, etc. Le but ici est de développer une compréhension conceptuelle de haut niveau de la TPE et de son fonctionnement. Pour un traitement plus approfondi de ces sujets, voir l’article original sur le TPE par J. Bergstra et ses collègues [1] .

Configuration de l’exemple

Pour construire notre implémentation de TPE, nous aurons besoin d’un exemple jouet avec lequel travailler. Imaginons que nous voulions trouver la ligne de meilleur ajustement à travers des données générées aléatoirement. Dans cet exemple, nous avons deux hyperparamètres à ajuster – la pente de la ligne m et l’interception b .

importer numpy en tant que np 

#Générer des données
 np.random.seed( 1 ) 
x = np.linspace( 0 , 100 , 1000 ) 
m = np.random.randint( 0 , 100 ) 
b = np.random.randint(- 5000 , 5000 ) 
y = m*x + b + np.random.randn( 1000 )* 700

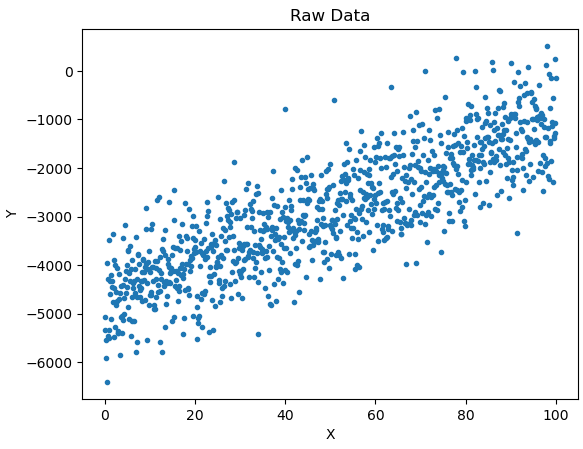
Étant donné que TPE est un algorithme d’optimisation, nous avons également besoin d’une métrique pour optimiser. Nous utiliserons l’erreur quadratique moyenne (RMSE). Définissons la fonction rmsepour calculer cette métrique comme suit :

def  rmse ( m, b ): 
    ''' 
    Consomme des coefficients pour notre modèle linéaire et renvoie RMSE. 
    
    m (float) : pente de la ligne 
    m (float) : ligne d'interception 
    y (np.array) : vérité terrain pour la prédiction du modèle 
    '''
     preds = m*x + b 
    return np.sqrt(((preds - y)** 2 ). somme ()/ len (preds))

La dernière chose dont nous aurons besoin, ce sont quelques croyances initiales sur ce que sont nos meilleurs hyperparamètres. Disons que nous pensons que la pente de la ligne de meilleur ajustement est une variable aléatoire uniforme sur l’intervalle (10,100) et que l’ordonnée à l’origine est également une variable aléatoire uniforme sur l’intervalle (-6000, -3000). Ces distributions sont appelées a priori. Qu’il s’agisse de variables aléatoires uniformes équivaut à dire que nous pensons que les vraies valeurs des meilleurs hyperparamètres sont également susceptibles de se situer n’importe où dans leurs intervalles respectifs. Nous allons implémenter une classe pour encapsuler ces variables et les utiliser pour définir notre espace de recherche initial.

class  UniformDist : 
    ''' 
    La classe encapsule le comportement pour une distribution uniforme. 
    ''' 
    def  __init__ ( self, min_, max_ ): 
        ''' 
        Initialise notre distribution avec les bornes fournies 
        '''
         self. min = min_ 
        soi. max = max_ 
        
    def  sample ( self, n_samples ): 
        ''' 
        Renvoie des échantillons de notre distribution 
        ''' 
        return np.random.uniform(self. min , self. max , n_samples)

#Définir l'espace de recherche des hyperparamètres
 search_space = { 'm' :UniformDist( 10 , 100 ), 'b' :UniformDist(- 6000 ,- 3000 )}

Une fois cette configuration terminée, nous pouvons passer au codage de l’algorithme lui-même.

Étape 1 : Exploration aléatoire

La première étape du TPE consiste à échantillonner au hasard des ensembles d’hyperparamètres à partir de nos a priori. Ce processus nous donne une première approximation de l’emplacement des zones de notre espace de recherche qui produisent de bons modèles. La fonction sample_priorsconsomme notre espace de recherche initial et un certain nombre d’échantillons aléatoires à en tirer. Il évalue ensuite les modèles résultants à l’aide de notre fonction objectif rmseet renvoie un Pandas DataFrame contenant la pente, l’interception et la RMSE de chaque essai.

import pandas as pd 

def  sample_priors ( space, n_samples ): 
    ''' 
    Consomme l'espace de recherche défini par les priors et renvoie 
    n_samples. 
    '''
     seed = np.array([space[hp].sample(n_samples) for hp in space]) 
    
    #Calculer rmse pour chaque paire d'intercepts de pente dans la graine
     seed_rmse = np.array([rmse(m, b) for m, b dans seed.T]) 
    
    #Concaténer et convertir en dataframe
     data = np.stack([seed[ 0 ], seed[ 1 ], seed_rmse]).T 
    essais = pd.DataFrame(data, columns=['m' , 'b' , 'rmse' ]) 
    
    retour essais

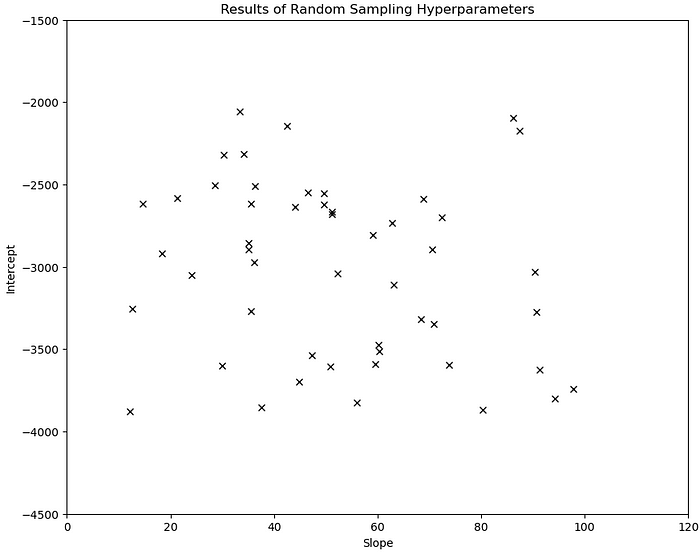
Étape 2 : Partitionnement de l’espace de recherche et estimation de Parzen

Après avoir généré quelques échantillons initiaux à partir de nos priors, nous divisons maintenant notre espace de recherche d’hyperparamètres en deux en utilisant un seuil de quantile γ, où γ est compris entre 0 et 1. Choisissons arbitrairement γ=0,2. Les combinaisons d’hyperparamètres qui aboutissent à un modèle qui fonctionne dans les 20 % supérieurs de tous les modèles que nous avons créés jusqu’à présent sont regroupées dans une “bonne” distribution l(x). Toutes les autres combinaisons d’hyperparamètres appartiennent à une « mauvaise » distribution g(x).

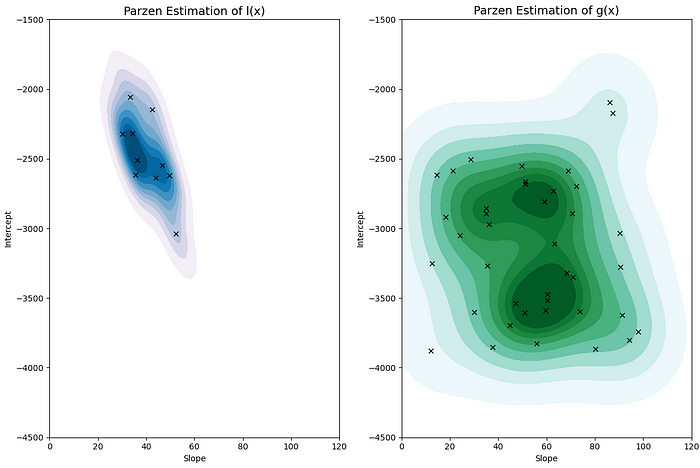
Il s’avère que la meilleure prochaine combinaison de nos hyperparamètres à tester est donnée par le maximum de g(x)/l(x) (si vous souhaitez voir la dérivation de ceci voir [1 ]). Cela a du sens intuitivement. Nous voulons des hyperparamètres hautement probables sous notre « bonne » distribution l(x) et peu probables sous notre « mauvaise » distribution g(x). Nous pouvons modéliser chacun de g(x) et l(x) à l’aide des estimateurs de Parzen, d’où vient le “PE” dans “TPE”. L’idée approximative de l’estimation de Parzen, alias Kernel Density Estimation (ou KDE), est que nous allons faire la moyenne sur une série de distributions normales chacune centrée sur une observation appartenant à g(x) ou l(x) (respectivement). Les distributions résultantes ont une densité élevée sur les régions de notre espace de recherche où les échantillons sont proches les uns des autres et une faible densité sur les régions où les échantillons sont éloignés. Pour effectuer l’estimation de Parzen, nous utiliserons l’ KernelDensityobjet de la bibliothèque SKLearn. La fonctionsegment_distributionsconsomme nos essais DataFrame et notre seuil γ et renvoie un estimateur de Parzen pour l(x) et g(x) chacun. Les distributions résultantes sont visualisées dans la figure 4.

from sklearn.neighbors import KernelDensity 

def  segment_distributions ( essais, gamma ): 
    ''' 
    Divise les échantillons en distributions l(x) et g(x) en fonction de notre 
    gamma de coupure quantile (en utilisant rmse comme critère). 
    
    Renvoie un estimateur de densité crénée (KDE) pour l(x) et g(x), 
    respectivement. 
    '''
     coupe = np.quantile(essais[ 'rmse' ], gamma) 
    
    l_x = essais[essais[ 'rmse' ]<coupe][[ 'm' , 'b' ]] 
    g_x = essais[~essais.isin (l_x)][[ 'm' , 'b' ]].dropna()
    
    l_kde = KernelDensity(kernel= 'gaussien' , bande passante= 5.0 ) 
    g_kde = KernelDensity(kernel= 'gaussien' , bande passante= 5.0 ) 
    
    l_kde.fit(l_x) 
    g_kde.fit(g_x) 
    
    return l_kde, g_kde

Étape 3 : Détermination des prochains « meilleurs » hyperparamètres à tester

Comme mentionné à l’étape 2, le prochain meilleur ensemble d’hyperparamètres à tester maximise g(x)/l(x). Nous pouvons déterminer ce que sont cet ensemble d’hyperparamètres de la manière suivante. Nous tirons d’abord N échantillons aléatoires de l(x). Ensuite, pour chacun de ces échantillons, nous évaluons leur log-vraisemblance par rapport à l(x) et g(x), en sélectionnant l’échantillon qui maximise g(x)/l(x) comme prochaine combinaison d’hyperparamètres à tester. L’ KernelDensityimplémentation SKLearn que nous avons décidé d’utiliser rend ce calcul très facile.

def  choose_next_hps ( l_kde, g_kde, n_samples ): 
    ''' 
    Consomme KDE pour l(x) et g(x), échantillonne n_samples à partir de 
    l(x) et évalue chaque échantillon par rapport à g(x)/l(x). 
    L'échantillon qui maximise cette quantité est renvoyé comme 
    prochain ensemble d'hyperparamètres à tester. 
    '''
     samples = l_kde.samples(n_samples) 
    
    l_score = l_kde.score_samples(samples) 
    g_score = g_kde.score_samples(samples) 
    
    hps = samples[np.argmax(g_score/l_score)] 
    
    return hps

Tous ensemble maintenant

Il ne nous reste plus qu’à enchaîner tous les composants discutés précédemment dans un seul algorithme et nous avons notre implémentation de TPE ! Les décisions que nous devons prendre ici sont le nombre de cycles d’exploration aléatoire que nous voulons effectuer, le nombre total d’itérations de l’algorithme que nous voulons effectuer et quel sera notre seuil de coupure γ (oui, même TPE a des hyperparamètres). Voici quelques éléments à prendre en compte lors du choix de ces quantités.

1. Si le « meilleur » ensemble d’hyperparamètres n’est pas capturé par vos priors avant de commencer TPE, l’algorithme peut avoir du mal à converger.
2. Plus vous effectuez d’explorations aléatoires, meilleures seront vos approximations initiales de g(x) et l(x), ce qui peut améliorer les résultats de tpe.
3. Plus la valeur de γ est élevée, moins il y aura d’échantillons dans l(x). Le fait de n’avoir que quelques échantillons à utiliser lors de l’estimation de l(x) peut conduire à une mauvaise sélection d’hyperparamètres par tpe.

def  tpe ( space, n_seed, n_total, gamma ): 
    ''' 
    Consomme un espace de recherche d'hyperparamètres, le nombre d'itérations pour l'ensemencement 
    et le nombre total d'itérations et effectue une optimisation bayésienne. Le TPE 
    peut être sensible au choix du seuil de quantile, que nous contrôlons avec gamma. 
    ''' 
    
    #Seed priors
     trial = sample_priors(space, n_seed) 
    
    for i in  range (n_seed, n_total): 
        
        #Segment trial in l and g distributions
         l_kde, g_kde = segment_distributions(trials, gamma) # 
        
        Déterminer la prochaine paire d'hyperparamètres à tester
         hps = choose_next_hps(l_kde, g_kde, 100 )
        
        #             Évaluer         avec la
         valeur efficace et ajouter aux essais in enumerate (trials.columns)},             ignore_index= True         ) renvoie les essais
        

 


        
    

Résultats

Pour effectuer TPE sur nos données synthétiques que nous avons créées précédemment, nous exécutons ce qui suit :

#Définir l'espace de recherche d'hyperparamètres
 np.random.seed( 1 ) 
search_space = { 'm' :UniformDist( 10 , 100 ), 'b' :UniformDist(- 6000 ,- 3000 )} 

df = tpe(search_space, 
         n_seed= 30 , 
         n_total= 200 , 
         gamma= .2 )

C’est ça! Nous pouvons maintenant analyser nos résultats. Par souci de concision, le code utilisé pour générer les visualisations suivantes ne sera pas affiché. Cependant, le code source peut être trouvé dans le référentiel GitHub pour ce projet.

Commençons par comparer notre meilleur ensemble d’hyperparamètres de TPE avec la meilleure pente et l’interception réelles d’un solveur de régression.

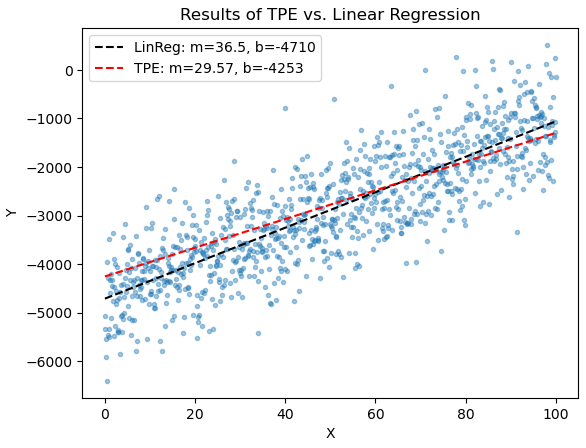
Comme nous pouvons le voir sur la figure 5, avec TPE, nous sommes en mesure d’approcher étroitement le meilleur ensemble d’hyperparamètres pour notre ligne. Nous ne nous attendrions pas à ce que TPE surpasse le solveur de régression car la régression linéaire a une solution de forme fermée. Cependant, sur un nombre infini d’essais, nous nous attendrions à ce qu’il converge vers une solution similaire.

TPE est un algorithme d’optimisation, donc nous ne nous soucions pas seulement d’avoir pu trouver un ensemble décent d’hyperparamètres. Il faut aussi vérifier que sur les 200 itérations notre fonction objectif décroît. La figure 6 montre qu’après nos 30 premiers échantillons aléatoires, notre implémentation de TPE procède à la minimisation de notre fonction objectif avec une tendance claire (plutôt).

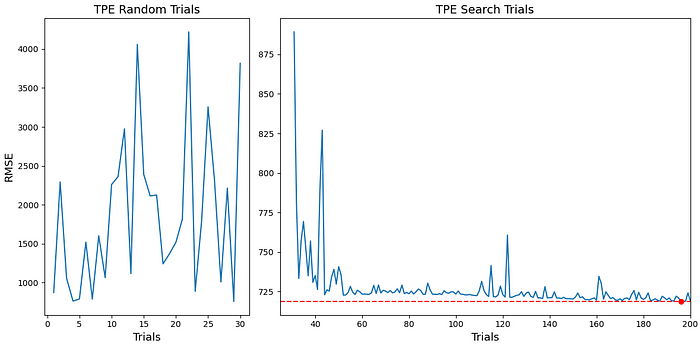
Jusqu’à présent, tout a l’air génial! La dernière chose que nous voulons vérifier est de savoir comment nos croyances sur la “meilleure” distribution de nos hyperparamètres ont changé au cours de nos 200 itérations.

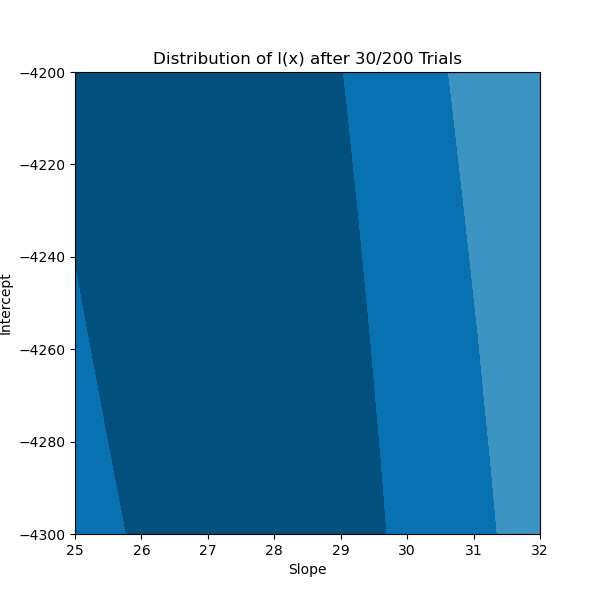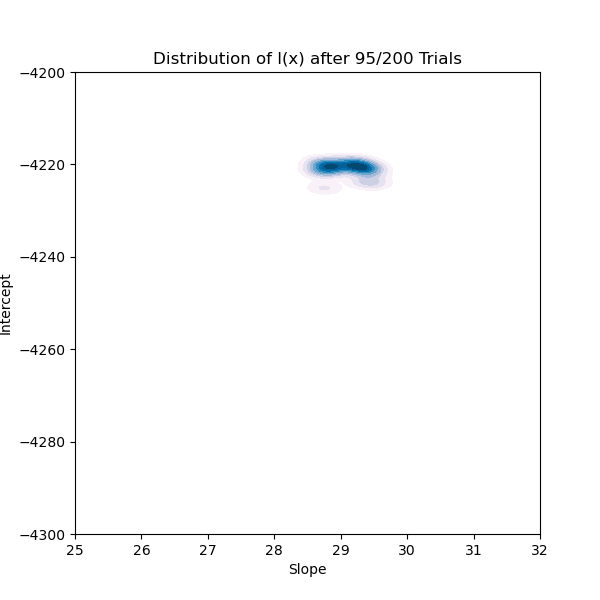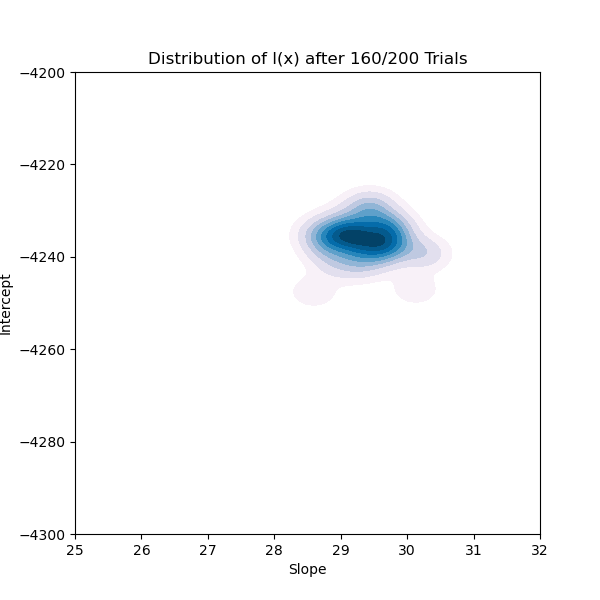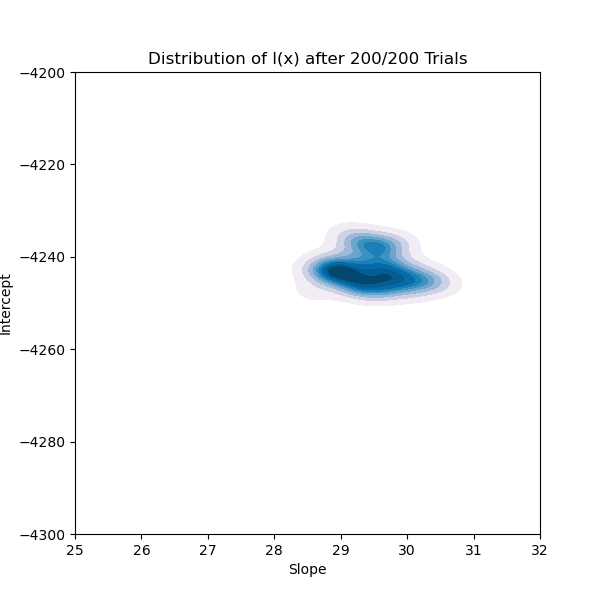
Comme nous pouvons le voir sur la figure 7, nous commençons avec une distribution très large de l(x) qui s’effondre rapidement jusqu’à quelque chose qui se rapproche de notre résultat final. Les figures 6 et 7 illustrent clairement comment chacune des trois étapes simples de TPE se combinent pour nous donner un algorithme capable d’explorer un espace de recherche de manière complexe mais intuitive.

conclusion

Le réglage des hyperparamètres est une partie essentielle du processus de modélisation. Alors que les approches de recherche de grille et de recherche aléatoire sont faciles à mettre en œuvre, TPE, en tant qu’alternative, fournit un moyen plus fondé de régler les hyperparamètres et est assez simple d’un point de vue conceptuel. Plusieurs bibliothèques Python existent avec de très bonnes implémentations de TPE dont Hyperopt (qui a été créé et est maintenu par les auteurs de [1]) et Optuna . Que ce soit pour quelque chose d’aussi simple que notre exemple de jouet ou d’aussi complexe que le réglage d’hyperparamètres pour un réseau de neurones, le TPE est une technique polyvalente, efficace et simple qui a gagné en popularité en science des données et en apprentissage automatique au cours des dernières années. La prochaine fois que vous vous retrouverez à régler les hyperparamètres de votre modèle, ignorez peut-être la recherche par grille.